Forget the smoky backrooms and gut-feeling bluffs. The modern poker landscape is a digital battleground, governed by complex algorithms and a branch of mathematics called game theory. At the heart of this revolution are poker solvers. These powerful programs don’t just calculate odds; they map out the very fabric of the game. But how do they actually work? Let’s pull back the curtain.
It All Starts with a Toy Game
You can’t just throw a full-scale, no-limit hold’em game at a computer and ask for the perfect solution. The number of possible decision points is astronomically huge—honestly, it’s a number so big it’s practically meaningless. So, researchers started small.
They created simplified “toy games.” Imagine a version of poker with only a 3-card deck, one round of betting, and a tiny stack size. By solving these miniature versions, mathematicians uncovered the core principles that could then be scaled up. It’s like learning to build a watch by first understanding a single gear.
The Core Engine: Nash Equilibrium and Counterfactual Regret Minimization
This is the real meat of it. Solvers aren’t trying to “win” in the way a human does. They are searching for a Nash Equilibrium (NE). In poker terms, an NE is a state where no player can improve their expected value by unilaterally changing their strategy. If everyone is playing at equilibrium, there’s literally nothing your opponent can do to exploit you. You become unexploitable.
But how does a computer find this mythical state? The most common algorithm is a beast called Counterfactual Regret Minimization (CFR). The name is intimidating, but the concept is, well, beautiful in its logic.
CFR works through self-play over millions of simulated hands. After each hand, it looks at every decision point and asks a simple question: “How much regret do I have for not choosing a different action?”
Think of it like this: You bet, your opponent folds. The solver then analyzes what would have happened—the counterfactual—if you had checked instead. If checking would have made more money on average, it accumulates “regret” for betting. Over countless iterations, the algorithm continuously adjusts its strategy to minimize this overall regret. Eventually, it converges on a mix of strategies where it has minimal regret for any action at any point. And that, you know, is the Nash Equilibrium.
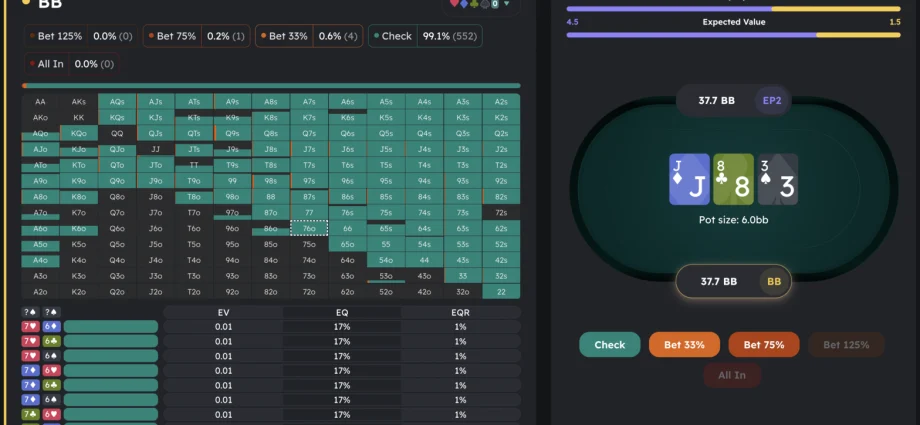
What Solvers Actually Output: It’s Not One Answer
This is a crucial point beginners often miss. A solver doesn’t give you a single “correct” move. It provides a range of hands to take each action with, and a specific frequency for doing so.
| Your Hand | Action from Solver | The “Why” |
| Pocket Aces (AA) | Bet 75% of the time, Check 25% | This balances your strategy, making you unpredictable. Checking sometimes protects your checking range. |
| 7-high flush | Bet small 100% | This hand is too weak to check; it needs protection and value from worse flushes. |
| Complete air (no pair) | Bluff 15% of the time | This frequency makes it impossible for your opponent to profitably exploit you by always folding. |
This mixed-strategy output is what makes GTO (Game Theory Optimal) play so robust. You’re not a pattern. You’re a probability distribution.
The Human Hurdle: Interpreting the Data
Here’s the deal: running a solver is one thing. Understanding the output is a whole different skill. The data can be overwhelming. You’re faced with massive range vs. range matrices and complex betting trees. The real art form is in the interpretation.
Why does the solver check back the top 10% of its range on this specific flop? Why does it use a tiny bet size with its strongest hands here? The answers are always buried in the mathematical relationships between the board texture, stack sizes, and the ranges of both players. It’s a puzzle. A brutally complex, mathematical puzzle.
The Limits and The Future
As powerful as they are, solvers have real limitations. They operate in a vacuum with perfect information about starting ranges. Real-world poker is messy. It involves:
- Player Tendencies: Why play an unexploitable strategy against someone who folds too much? Humans must adapt.
- Computational Boundaries: Even with supercomputers, true Nash Equilibrium for a full no-limit hold’em game hasn’t been “solved.” The approximations are just incredibly, incredibly good.
- Intangible Factors: Tilt, table dynamics, fatigue—none of this exists in the solver’s pristine world.
That said, the technology is still evolving. We’re seeing the rise of real-time assistance software (RTA), a controversial edge where players consult solvers mid-game. And machine learning is being integrated to create more adaptive, “human-like” AI that can adjust to exploits on the fly.
So, What Does This Mean For You?
Honestly, you don’t need to understand the deep math of CFR to benefit from solver technology. But grasping the core concepts—Nash Equilibrium, ranges, and frequencies—is the key to modern poker literacy. It changes how you view the game. It’s no longer just about your two cards and the board. It’s about the entire universe of possible hands, the intricate dance of probabilities, and finding a strategy that remains solid no matter what storm comes your way.
The solver is the ultimate theorist, revealing the game’s fundamental blueprint. The best human players are the architects who take that blueprint and build something that can withstand the chaos of a real-world fight. The mathematics provides the map, but you still have to navigate the terrain.